Thoughts on Automata Theory
I’ve been reading many texts on automata theory these times, and let me tell you, that’s such a wonderful thing. It pretty much explain how computers can…. compute! Simply put, Automata Theory deals with the logic of computation with respect to simple machines, referred to as Automata.
From the mathematical models to represent it to the fun programming implementations, it’s really great and exciting to study it!
Automatons are abstract models of machines that perform computations on an input by moving through a series of states or configurations. At each state of the computation, a transition function determines the next configuration on the basis of a finite portion of the present configuration. As a result, once the computation reaches an accepting configuration, it accepts that input. The most general and powerful automata is the Turing machine.
In layman’s terms, FSM (Finite State Machine) or Automaton is a device (hardware or software) that responds to external events and produces actions. The actions generated depend on the past history of the system, i.e. its state.
This can go from a simple reserved word analyzer
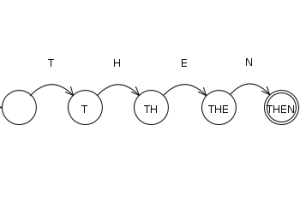
To big Regular Expressions:
Automatons are also essentials to understand the limits of the computation, thus, we have now two important problems coming out from this thought:
1. What computers can do?
2. What computers can do efficiently?
The first one is called Decidability and the second one is called intractability
And it brings our minds to the very beginning of the Computing Science, where many scientist were thinking about the limits of computation, not that today there aren’t many scientists working on it, but today many programmers, sadly, ignore this kind of knowledge.
But, returning to our automatons, they’re represented by a bunch of states that we represent formally as \( Q \), a finite set of symbols ( \( \sum \) ), a transition function ( \( \delta \) ) that has two parameters: a state \( Q \) and a symbol, this function is responsible for the change of states in the automaton. An initial State from \( Q \) and a acceptance state also from \( Q \).
So we can say that a generic automaton can be represented formally as
$$ A = \left ( Q, \sum, \delta, q0, F \right ) $$
The automatons fall into two classifications, they can be:
Deterministic
Where they can’t be at more than one state at the same time, it’s the real world way to represent abstracts machines, because this kind of automaton has no ambiguity . Here’s a simple example of an DFA (Deterministic Finite Automaton) that only accepts string having 001 as substring.
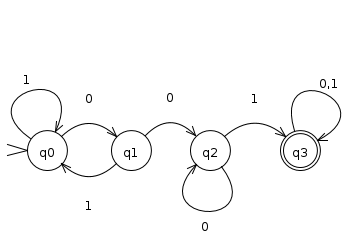
Informally speaking, if you put a string of 0s and 1s such as 10011 and process it number by number, following the states changes you will see that it will end the processing and your current state will be the acceptance state, so, this string is acceptable! So a string such as 11101010, if you try the same process, won’t end at an acceptable state, so we say that this string is not acceptable by this automaton.
Non Deterministic
In this case, the automaton can change to multiple states at the same time, which means, it’s not so deterministic and precise as the deterministic automaton. So why one would use this non deterministic automaton? Simply put, it’s way easier to design a NFA (Non deterministic Finite Automaton) to solve a determined problem than to design a precise DFA to solve this same problem.
But! We’ve a problem here!
How can a computer, which is an unambiguous machine, process something that is not deterministic?
It can’t. And it won’t!

So why in the seven hells would i want to use this NFA if the machine can’t understand?
The answer is, every NFA has an equivalent DFA, which means, if a language is recognized by the NFA and by the DFA, they’re equivalent. All you have to do is translate the NFA into a DFA so the machine can use it!
Talking about Language, what is it in this context?
Well, this is what we call Regular Language which is a Language L accepted by an Automaton, so the language of an Automaton is the set of all string that it accepts.
We can define the language of a DFA as
$$ L(A) = { \omega ,|, \delta(q0, \omega), is, in, F } $$
Which means, an Automaton processing a string, from its initial state, being computed by its transition function, if the processing ends in the acceptance state, this means that this is the language of this DFA.
Conclusion, next steps and further readings
As you may have noticed, there are unimaginable ways to use Automatons, it wasn’t even created to apply directly in the Computer Science, two neurophysiologists, were the first to present a description of finite Automata in 1943. Their paper, entitled, “A Logical Calculus Immanent in Nervous Activity”, had a huge impact in the computer science.
For anyone who’s trying to dive deeper in this field, I strongly advice the Ullman’s book on Automata and Complexity Theory
And soon I pretend to write few more thing on Automata, such as techniques to translate a NFA to a DFA using the algorithm of subset construction.
For now my main goal was to simply introduce this beautiful branch of the Computer Science and Mathematics and show its applications.
If something isn’t clear to you, drop me an email and let’s talk about it! :)