Graph Theory is definitely one of my favorite branches of the Mathematics & Computer Science, mostly because of its nearest infinity applications, in both real world problems and pure theoretical problems.

These days I’ve been working (with my buddy Daniel Almeida) in a framework to create and manipulate graphs. Which means, creating a data structure to represent graphs, edges, vertexes and creating algorithms to work on this structure. All this is being made with Java and I’ll expose this code here, as I saw a terrible lack of good readable codes about it on the internet.

So, before we start coding the graph’s structure… we must clarify what a graph is and why it’s so important to the Computer Science (and many other sciences).

A graph is a ordered pair (G = (V,E)) , where (V) is a set of Vertices/Nodes and (E) is a set of Edges, an extremely mple example of a complete simple, connected and complete graph is:

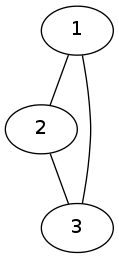
So, what’s the huge deal with this graph theory thing?

Well, not only theoretical computer science problems lay on the graph theory but also in many other distinct fields, from particle physics, chemistry to sociology.

All this because every little thing in our universe is linked, and when this set of things became a “web of things”, we need to study its properties. And that’s where graph theory get in.

So when a graph gets bigger, we need to represent this structure in a computational way, so we can compute things like shortest path between two nodes, connectivity and thousand of other properties and techniques.

The most common ways to represent graph mathematically are:

Adjacency Matrix

It’s a matrix that represent the adjacency of every node in a graph, it’s an excellent way to work computationally with graphs. The same graph that I presented previously in a visual way can be represented by the following adjacency matrix:

$$ \begin{bmatrix} 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \end{bmatrix} $$

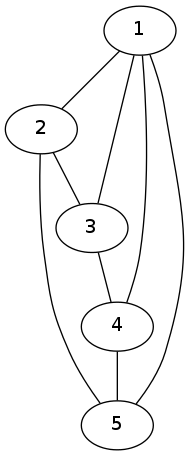
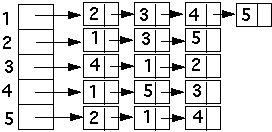
Adjacency List

This is another common way to represent graph mathematically, it’s a simple list of lists, each node in the main list points to a list of their adjacent nodes.

Here’s an example:

Data Structures to represent Graphs

Ok, so, how do we represent graphs, edges and vertexes in terms of data structures? Before we dig deeper in the algorithms and the mathematical properties of the graphs, we need to create our Data Structure to work with.

The vertex

For now you may be asking yourself why do we need a variable called “Visited”. Well, we’ll be using it in algorithms to walk through the graph, so we must need to know which nodes were visited. It will became more clear soon!

The Edge

Yes, the edge must be represented computationally! That’s our way to figure out paths through the vertexes, the edge may or may not have a weight, the edge must know its source vertex and its destination vertex

The Graph

That’s for sure the biggest and most complex part, don’t panic with the many algorithms already implemented in this code. I’ll be explaining one by one.

We’re reading a text file containing the text file, if you want to test by yourself, make sure to create a .txt in the correct way and to pass the correct file path! You can find the instructions to write the .txt graph in the comments of this code

The test file

Here’s the file containing the main, if you want to test, remember to change the path file!

Conclusion and next steps

At this moment, you’re perfectly able to create a graph (via .txt file) and run all those algorithms to extract information about your graph. Just make sure to import the right libraries and to put the files in the right package. Doing these little things right, I’m pretty sure this will work perfectly.

But I’m sure you may be a little lost about a few algorithms and techniques we’ve implemented in the Graph.java. But, don’t worry, i’ll be explaining each method one by one in the next parts of this post!